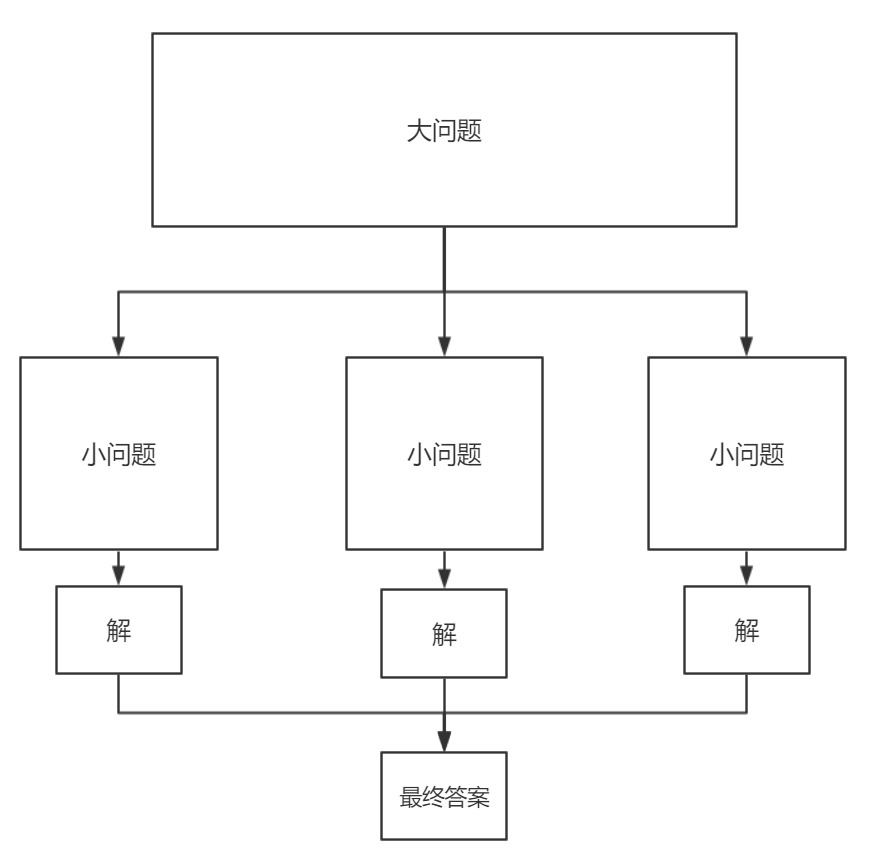
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解,是一种分目标完成程序算法,简单的问题可用二分法完成。
1. 分治算法
我们在使用分治算法求解问题的时候是把一个问题划分为多个小问题,然后通过各个小问题的答案来找到合适的,如果数据规模还是比较大,那么可以再进行一次分治算法,直到找到答案为止。
分治算法的解题步骤一般如下:
(1)分解,将要解决的问题划分成若干规模较小的同类问题;
(2)求解,当子问题划分得足够小时,用较简单的方法解决;
(3)合并,按原问题的要求,将子问题的解逐层合并构成原问题的解。
2. 求n个元素中的最小值
一个列表中存在n个数据的时候,找到其中的最大值,当然这个问题我们使用Python可以直接通过max()函数和min()函数来解决,在这里我们使用分治算法来解决这个问题。
问题分析,如果这个问题的数据规模小于等于2的时候,我们可以经过一个判断就找到其中的最小值,所以我们需要做的就是想办法把这若干个数据变成两个数据进行比较,那么我们可以先把数据从中间划分为左右两部分,然后通过递归再把每一部分再划分为左右两部分,直到数据规模小于等于2的时候,返回结果,然后通过递归到最后为两个数据对比,我们就可以找到最小值。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | def get_max(number):#寻最小值函数 if len(number) == 1 return number[0] else: if number[1]>number[0]: return number[0] else: return number[1]# 分治法def solve(number): n = len(number) if n <= 2: # 数据规模小于等于2使用get_max()函数 return get_max(number) # 分解(子问题规模为 n/2) left_list, right_list = number[:n // 2], number[n // 2:] # 递归(树),分治 left_max, right_max = solve(left_list), solve(right_list) # 合并 return get_max([left_max, right_max])if __name__ == "__main__": # 测试数据 test_list = [33,52,2,25,63,75,43,72,45,97,53,25,14,18,3,5] # 求出最小值 print(solve(test_list)) |
输出结果为:
1 | 2 |
3. 找到一组数据中第 k 小的元素
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | def divide(number):# 划分函数 fis = number[0]#定义一个主元 litter = [x for x in number[1:] if x < fis]#比主元小的元素存放一个列表 big = [x for x in number[1:] if x >= fis]#比主元大的元素存放一个列表 return fis,litter,bigdef find(number,key):# 查找第 k 小的元素 fis,litter,big = divide(number) #分解 n = len(litter) if n == key: return fis#找到 elif n < key: return find(big,key-n-1)#递归分治 else: return find(litter,key)#递归分治if __name__ == '__main__': list = [3, 45, 18, 65, 53,15,26,37, 27, 49, 17, 93, 0, 100, 13, 62, 52, 7, 24, 29] print('第5小的元素:',find(list,5)) print('第10小的元素:',find(list,10)) |
输出结果为:
1 2 | 第5小的元素: 17第10小的元素: 29 |
4. 总结
关于分治算法,它的实质就是将每个子问题独立,然后递归求解,来帮助我们解决数据规模较大的问题,它的缺点在于当子问题不独立的时候就需要求公共子问题,所以我们在运用的时候一定要考虑一下是否适合分治算法。
